Assumptions in Strength Design Method for Flexure

These assumptions were organized based from Fanella (2011). These assumptions will be a guide in deriving the formulas that will be used in the analysis of concrete beams.

1. The strains in the reinforcement and the concrete shall be assumed directly proportional to the distance from the neutral axis. Except for deep flexural members with overall depth to clear span ratio, h/L>2/5 for continuous spans and h/L > 4/5 for simple spans, a nonlinear distribution of strain shall be considered.
2. The maximum usable strain at the extreme concrete compression fiber is 0.0030.
3. If the stress in the reinforcement \(f_s\) below its specified yield strength \(f_y\) is equal to the modulus of elasticity of the steel \(E_s\) time the steel strain \(ε_s\). However, the stress in the reinforcement is equal to \(f_y\) for strains \(ε_s\) greater than or equal to \frac{f_y}{E_s}.
4. The tensile strength of concrete is neglected in the axial and flexural calculation of reinforced concrete.
5. The relationship between the concrete compressive stress distribution and the concrete strain shall be assumed to be rectangular.
6. For Rectangular distribution of stress, see Figure 2-1.

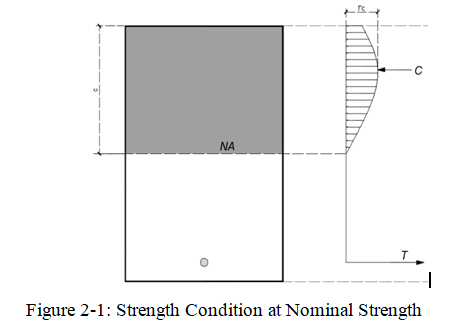
• Concrete stress of 0.85f’c shall be assumed uniformly distributed over an equivalent compression zone bounded by edges of cross-section and a straight line located parallel to the neutral axis at a distance of a=β_1 c from the fiber of the maximum compressive strain.
• The distance(c)of the neutral axis (NA) from the fiber of maximum shall be measured in the direction perpendicular to the NA.
• Factor \(β_1\) shall be taken as 0.85 for \(f'_c \leq 30\) MPa and \(β_1\) shall be reduced continuously at a rate of 0.008 for each 1 Mpa of strength in excess of 30 MPa but \(β_1\) shall not be taken less than 0.65.

- For \(f'_c \leq 28 MPa\), \(β_1=0.85\)

- For \(f'_c > 30 MPa\), \(β_1=0.85-0- \frac{1}{140}(f'_c-28) \) but not less than 0.65.

Research shows that the concrete stress distribution above the neutral axis (NA) is parabolic. However, the code permits the use of an equivalent rectangular concrete stress distribution. According to Whitney (1942), the parabolic stress block can be reduced to a rectangular stress block. However, in reducing the initial value \(f'_c\) of the parabolic stress block will be reduced to \(0.85f'_c\) and the depth a less than c; see Figure 2-2.

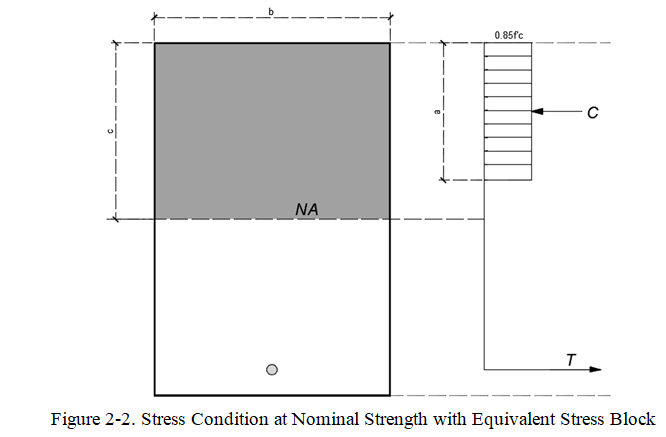
Furthermore, the code specified that \(a = β_1 c \) and from Table 419.2.1.1 of NSCP 2015, the minimum \(f'_c\) of Normal weight concrete for Special Moment Resisting Frames and Special Structural walls is 21 MPa. Using Figure 2-2, the resultant compression stress (C) in the concrete is the volume of the concrete stress block, thus;

\(C=0.85f'_c ab\)

Where:
\(f'_c\) is the compressive strength of the concrete,
\(a\) is the depth of the stress block
\(b\)is the width of the beam

Also, the tensile stress on the reinforcement can be calculated as the product of the yield strength \(f_y\) of the reinforcement and its area \(A_s\).

\(T = A_s f_y\)

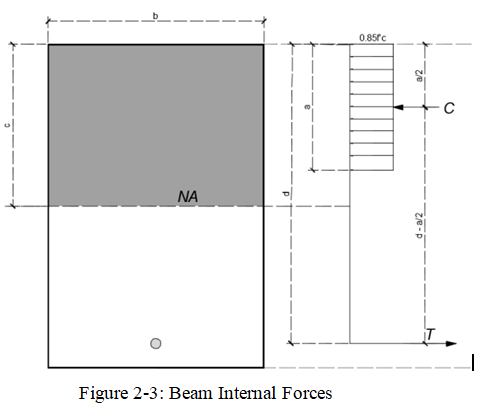
Using Figure 2-3, for the system to be in equilibrium, the summation of forces must be equal to zero.

\(\sum F_h = 0\)

\(C = T\)

\(0.85 f'_c a b = A_s f_y\)

\(a = \dfrac{A_s f_y}{0.85 f'_c b}\)

\(a = \dfrac{A_s f_y}{0.85 f'_c b} \cdot \dfrac{d}{d} = \dfrac{A_s}{b d} \cdot \dfrac{f_y d}{0.85 f'_c} = \rho \dfrac{f_y d}{0.85 f'_c}\)

\(\rho = \dfrac{A_s}{b d}\), the steel ratio or the percentage of tensile steel.

The nominal strength of the beam \(M_n\) is the capacity of the beam based on its properties. The code permits the use of capacity with the consideration of a reduction factor(∅), thus the ultimate capacity \(M_max\) of the beam would be, \(M_max= ∅M_n\). This ultimate capacity should not be exceeded by the calculated factored moment \(M_u\) caused by factored loads. Thus,

\(M_u \le ∅M_n\)

The inequality simply indicates that the loads should not exceed the capacity of the beam. Figure 2-3 shows the internal forces acting on the beam. The moment generated when a moment is taken at C and T is the nominal moment \(M_n\). In this case, we would like that the concrete and the reinforcement will reach their ultimate capacity at the same time. Thus,

\(M_n=T(d-\dfrac{a}{2})=C(d-\frac{a}{2})\)

\(M_n = 0.85 f'_c a b (d - \tfrac{a}{2})\); \(a = \rho \dfrac{f_y d}{0.85 f'_c}\)

\(M_n = 0.85 f'_c b \left( \rho \dfrac{f_y d}{0.85 f'_c} \right) \left( d - \dfrac{\rho f_y d}{2(0.85 f'_c)} \right)\)

\(M_n = \rho f_y b d \left( d - \dfrac{\rho f_y d}{1.7 f'_c} \right)\)

\(M_n = \rho b d^2 f_y \left( 1 - \dfrac{\rho f_y}{1.7 f'_c} \right)\)

\(M_u = \phi M_n\)

\(\phi \rho b d^2 f_y \left( 1 - \dfrac{\rho f_y}{1.7 f'_c} \right) = M_u\)

\(\rho^2 \left( \dfrac{\phi b d^2 f_y^2}{1.7 f'_c} \right) - \rho (\phi b d^2 f_y) + M_u = 0\)

\(\rho^2 - \rho \dfrac{1.7 f'_c}{f_y} + M_u \left( \dfrac{1.7 f'_c}{\phi b d^2 f_y^2} \right) = 0\)

\(\rho^2 - \rho \dfrac{1.7 f'_c}{f_y} + \left( \dfrac{1.7}{2} \dfrac{f'_c}{f_y} \right)^2 = \left( \dfrac{1.7}{2} \dfrac{f'_c}{f_y} \right)^2 - M_u \left( \dfrac{1.7 f'_c}{\phi b d^2 f_y^2} \right)\)

\(\left( \rho - \dfrac{0.85 f'_c}{f_y} \right)^2 = \left( \dfrac{1.7}{2} \dfrac{f'_c}{f_y} \right)^2 - M_u \left( \dfrac{1.7 f'_c}{\phi b d^2 f_y^2} \right)\)

\(\rho = \dfrac{0.85 f'_c}{f_y} \pm \sqrt{ \left( \dfrac{0.85 f'_c}{f_y} \right)^2 - M_u \left( \dfrac{0.85 (2) f'_c}{\phi b d^2 f_y^2} \right) }\)

\(\rho = \dfrac{0.85 f'_c}{f_y} \pm \sqrt{ \left( \dfrac{0.85 f'_c}{f_y} \right)^2 \left( 1 - \dfrac{2 M_u}{0.85 \phi b d^2 f'_c} \right) }\)

\(\rho_1 = \dfrac{0.85 f'_c}{f_y} + \sqrt{ \left( \dfrac{0.85 f'_c}{f_y} \right)^2 \left( 1 - \dfrac{2 M_u}{0.85 \phi b d^2 f'_c} \right) }\)

\(\rho_2 = \dfrac{0.85 f'_c}{f_y} - \sqrt{ \left( \dfrac{0.85 f'_c}{f_y} \right)^2 \left( 1 - \dfrac{2 M_u}{0.85 \phi b d^2 f'_c} \right) }\)

In the derived equation for ρ, consider the negative root since, if the positive root is used, the ratio would be large. However, we would want to have the minimum steel as our reinforcement thus, we consider the negative to get the smallest possible steel needed.

\(\therefore \boxed{ \rho = \dfrac{0.85 f'_c}{f_y} \left( 1 - \sqrt{1 - \dfrac{2 M_u}{0.85 \phi b d^2 f'_c}} \right) }\)

• ACI Committee 318. (1995). Building code requirements for structural concrete : (ACI 318-95) ; and commentary (ACI 318R-95).
• Association of Structural Engineers of The Philippines. (2016). National structural code of the Philippines (NSCP) 2015 (7th ed.- 2nd printing).Association of Structural Engineers of the Philippines.
• Farmington Hills, MI : American Concrete Institute
• Fanela, D. (2011). Reinforced Concrete Structures Analysis and Design. The McGraw-Hill Companies.
• McCormac, J. C. (2005). Design of reinforced concrete (7th ed.). John Wiley & Sons.
• Nilson, A. H., & Darwin, D. (2010). Design of Concrete Structures (12th ed.). McGraw-Hill.
• Wright, J. K. (2021). Reinforced Concrete Mechanics and Design (7th Edition). Pearson Higher Ed